2Pnt Hermite Investigation - 01


Maya 2 Point HermiteSpline - Part 01

hermiteTest

PREFACE:

Over the last year in my spare time I've been doing some investigations in getting a couple of nodes worked out at home.
As it turned out, I haven't had a lot of spare time, as last year the show I was on was pretty challenging time wise etc.
So this year I thought I'd back track a little through my code and wth while I'm at it throw up a post or 2 about what I've been up to re looking into getting these nodes up and running [for better or for worse!]

DISCLAIMER: I'm still pretty new to c++ so I wouldn't rely "too heavily on the code snippets etc. But the nodes are performing/ behaving pretty well at the moment for me.
I should also highlight that I had *NO* idea about hermite stuff before I worked with Raffaele at Animal Logic.
If you're interested in rigging by first principles I highly reccomend you head over to Cult of Rig and watch Raf's streams.
These are packed full of good info and you can flick him a few bucks via patreon to show support!

Why hermite?

Well you can do some pretty cool things with a well written node. Some of the things but not limited to;
  • Running the hermite curve down the arms and legs for twist
  • Length preservation along ropes etc
  • General deformation in areas like the face etc

    What was my initial goal?

  • To investigate the creation of a node in Maya to take 2 inputs and ouput #n of output transforms(to drive joints) that represent a hermite spline with twist to use in rigs.
  • To try to make sure this can be run in parallel in Maya.
  • Extend this node to handle and array of inputs to define the curve.

    What were(are) my hurdles?

  • Little to no C++ experience (In maya or out of)
  • No idea about hermite math / math in general / curves!



    What is a hermite?

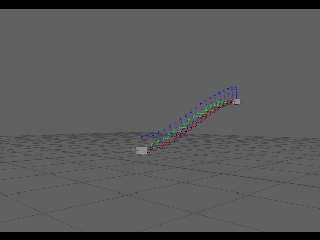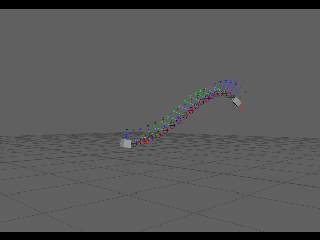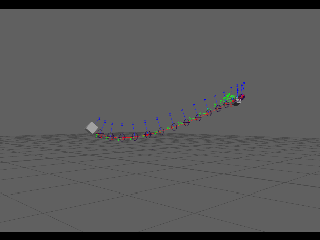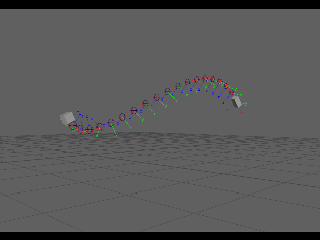
    Hermite interpolation is a way to define a curve. We can use this interpolation to create a new type of curve in maya for use in rigging. Therefore;
    First up I had to look into and try to figure out what the heck a hermite was from a math stand point!

    Wikipedia states:
    "In numerical analysis, Hermite interpolation, named after Charles Hermite, is a method of interpolating data points as a polynomial function."

    But sweet baby jesus it gets confusing fairly quickly on wikipedia.

    When looking further into this, I found cubic.org; which states:
    "To calculate a hermite curve you need the following vectors:
    P1: the startpoint of the curve
    T1: the tangent (e.g. direction and speed) to how the curve leaves the startpoint
    P2: the endpoint of the curve
    T2: the tangent (e.g. direction and speed) to how the curves meets the endpoint

    ...and the base functions for the hermite are:
    h1(t) = 2t^3 - 3t^2 + 1
    h2(t) = -2t^3 + 3t^2
    h3(t) = t^3 - 2t^2 + t
    h4(t) = t^3 - t^2
    Note: I changed s to t to represent (t)ime.
     These 4 vectors are simply multiplied with 4 hermite basis functions and added together."

    Brilliant! Someone broke it down to some fairly straight forward (math) basics. Much <3!!
    Essentially, because to begin with I have reduced the problem down to just 2 input points we can start at point1's position in worldSpace and end at point2's position in world space. Thus t0 = p1 and t1 = p2.

    So what does this mean for the node?
    At it's most basic form, we need to create a node in maya with just 2 inputs...
  • get their positions (p1, p2)
  • and 2 tangents T1, T2 [and for simplicity use a specific axis from each point as these tangents].
  • since length is going to be 1 we can work out the increment (time intervals for the outputs) by dividing the length by the number of outputs minus 1.
    increment = length / outputCount-1.

    This should give us a 2point hermite curve with a UNIFORM distribution of the outputs along the curve.
    Seems easy enough!? Right?
    [... part02](/c++/2018/04/03/hermite02.html)