2Pnt Hermite Investigation - 02

Maya 2 Point HermiteSpline - Part 02

Basic node jbd_hermite: .h

So first up I needed to get a shell of the node organised. Designing the interface for the node is as good a place as any.
So I'm going to need (as per part01 of this `thread');

2 points, and their tangents

#n of outputs

assumed length of 1

So a basic header ended up looking like this;
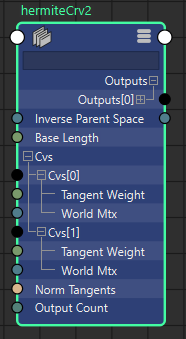
Now the quirky part here on initial inspection is that I chose to go with inPuts instead of p0 and p1. I did this because I want to extend this to be a hermiteArray later on accepting #n of input points, but for now I will only pull index 0 and 1 from the array for this node.
So inPuts will be an array with each element in the array consisting of;

inMatrix

inTangentWeight [The multiplier of the tangent]

And outputs will become an array of outputs with each element in the array consisting of;

• outMatrix
• outTranslate [as a nAttr.createPoint with x y z]
• outRotate
• outRotateX
• outRotateY
• outRotateZ
• outScale [as a nAttr.createPoint with x y z]

Later on I added the inverseParent, baseLength and normalizeTangents as per the png above, mainly because I wanted to be able to just normalize the tangents to a length of 1 with a click, make sure the node was always localized to the rig and perhaps at some point set it to be only along the curve to a time value of .5 instead of 1.

Basic node utils: .cpp

So here's where it got interesting, [and where my lack of c++ experience gets a bright light shined on it] in my spare time. The problems I faced here was how to handle all the code in the compute cleanly so my brain didn't explode!
Essentially I ended up building a utils.cpp with the following;
This helped me reduce the code for the hermite equations into inline calls which to me at the time made more sense.
From there I built a function to use these from the compute. Remember back in post 1 "These 4 vectors are simply multiplied with 4 hermite basis functions and added together." That essentially is what I am using this function for.

p1(3,0) is point1's tx from the matrix, and p1(3,1) is point 1's ty from the matrix etc
p2(3,0) is point 2's tx from the matrix, and p2(3,1) is point 2's ty from the matrix etc

I also made the decision to go along with vectors over a matrix math approach because well gotta start somewhere right?

Basic node jbd_hermite::compute: .cpp

I'm going to ignore the whole node initialization of the node as this isn't really that kind of post, and skip straight to the compute.


*NOTE: The below snippets of code cover the translate aspect of the node only.* Here I created a struct for storing the point data for use in the later iterator.
Note: This is more a descision for sanity and keeping my code it clean later on, and tbh I'm not entirely across the impact performance wise if this is a bad idea or not but my brain hurt less because of it. At the moment it makes sense to avoid having to jump through the array index 0 and 1 each time I loop through the outputs, instead just pulling the data directly from the previously formed struct data. Should be faster??

---

Here we want to exit early if we don't have a cv count of 2. If we have a cv count of more than 2 at this point I don't care cause I'm only pull index 0 and 1 from the array and everything else is ignored.

---

Here I'm leveraging the struct and pushing the data I want to call later on in the iterator as I go through all the outputs.
Note: I'm using the XTangent of the matrix as the hermite tangent!
This does create a need for rigging to mind map the axis correctly when setting up a rig with the node, but it's not too hard for them to remember.

---

So we iter through the outputCount -1 because we start at 0 which counts as an output, and we use the increment to step along the curve uniformly for the #outputs we want to distribute along the curve.

---

Final Notes:

Consider:
10 outputs distributed along a curve of len 10.0f. The increment becomes 10.0f/9.0f = 1.111

for(unsigned int i=0;

The iterator already starts at 0 which counts as one output, so we need to finish the iterator at outCount-1 or we end up with one output more than we need.
And that's it! Now we have the foundation for a hermite curve setup in maya. The interesting part here being that you can daisy chain this node and the curve will extend seamlessly;
eg:

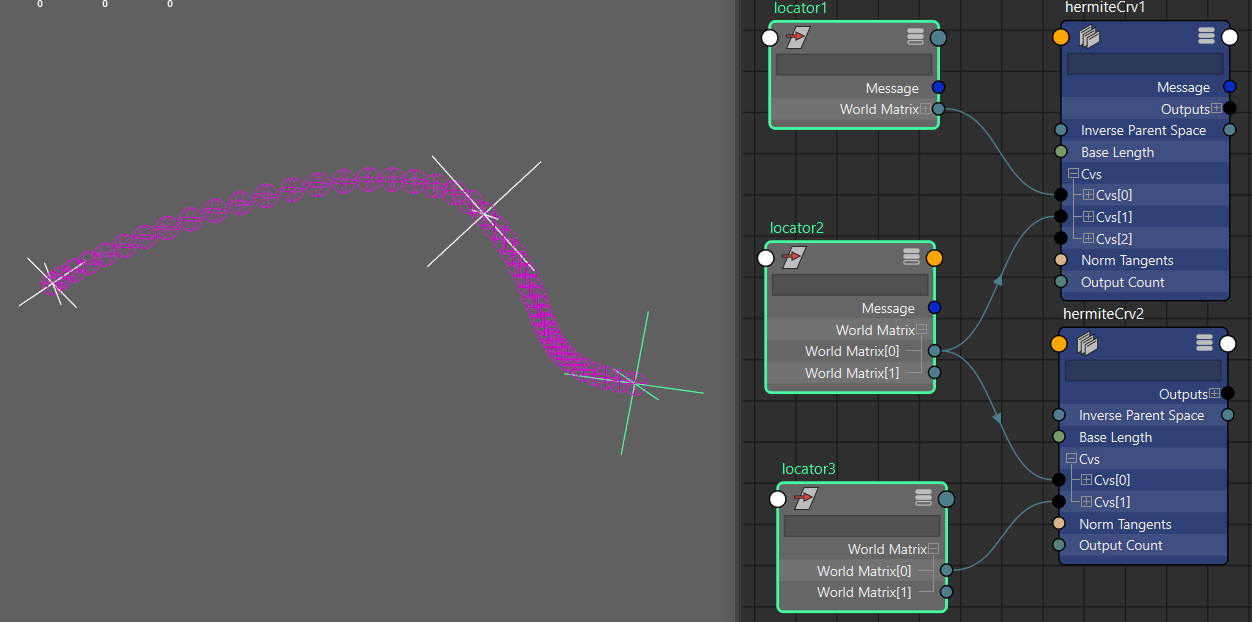
Now obviously for more complex rigs daisy chaining tons of nodes can be a pita, which is the reason I went with the array for the inputs so I could extend this node to accept #n of inputs to work out the hermite along in a single node.
Note: In the image above, because I am using the worldMatrix[0] from the locators I later put into the node the inverseParentSpace so I can localize the calculations to avoid any floating point precision issues when rigs are animated far away from origin (0,0,0)


And this is a look at the node working with rotation and scale for the tangents... pretty cool!
Profiling the node on that scene (total of 44 ouputs to drive the joints):
DG: 150fps
Serial: 312.5fps
Parallel: 365.9fps